Most of us were taught from a young age that one of the best ways to learn is to learn from our mistakes. However, this wise adage is rarely translated into testing and teaching methodologies in our educational system. Students are often given only once chance to be tested on a topic, in the format of intimidating exams which comprise large percentages of the grade they receive in any given class. Afterwards, a student is able to see the mistakes they’ve made from comments and feedback their instructor provides, yet they still suffer the consequences of errors they may have made from a not receiving a perfect score the first time around. Thus, even though a student may improve their understanding of a topic part-way through their progress in the class, this improvement is often not reflected in their grade. Grades, as we know, are meant to be the best representation of a student’s overall understanding of the topic; and we must then ask, how can a grade be truly representative of a student’s learning if it does not account for the academic developments they make? This is one of the motivations behind the very unique learning and grading system implemented by Professor Tyler Reese, a mathematics instructor at Foothill College.

The Idea

Tyler Reese is a cinematographer-turned-mathematician who first taught middle and high school mathematics before graduating from CSU East Bay with his Master’s degree in Applied Mathematics. Afterwards, he came to Foothill, and has been teaching Calculus 1A and 1B this past quarter. When I first arrived in his Calculus 1B class, it didn’t take me long to realize that he did things quite differently from any other teacher I’d previously encountered. The most notable difference in Professor Reese’s system to any math class I’d ever taken was his implementation of a retest policy in his class. Professor Reese’s class is structured around standards-based grading, where each section we learn about in class is given a mastery evaluation on a scale of 0-4. We would be assessed on our progress of these standards on a weekly basis, but here was the surprise — if we were unsatisfied with the mark we received on any particular standard, we would be allowed to retest on that topic, as many times as we wanted. The new grade we received would comprise 75% of the overall grade we earned on that standard, while the previous make would make up 25% (for example, if I received a 3 on a standard and them retested to receive a 4, my overall grade for that standard would be a 3.75.) In order to receive an overall grade of an A in Professor Reese’s class, a student needs to average a 3.5 across the board on all their standards. While this may seem easy enough, a student can only receive a grade of 4 if they make virtually no mistakes on a standard, and can prove that they truly have mastered the section.

How The Idea Developed

I decided to interview Professor Reese to learn more about this peculiar grading and retest system and his motivations behind setting it up. He described to me that as he was teaching middle school mathematics and seeing his students frustrated with their constant mistakes, he began researching more progress-based methods of teaching. The more he taught, the more he began to believe that learning and grading were two separate and exclusive entities that didn’t require each other. Despite this, as an educator, he was required to produce a grade for each of his students; so he experimented with a method that would best correlate the true learning process with a grade. “And here’s where it hit me,” Professor Reese described,

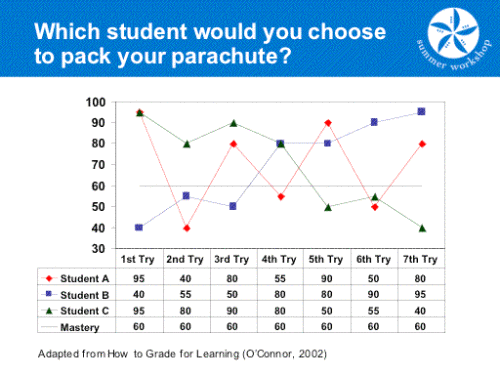
“There was a graphic that showed, ‘Who would you want to pack your parachute?’ There was one person who packed it perfectly the first time, but didn’t do it well the next time, did alright the next time, and so on. And would you want to jump out of a plane if the person who packed your parachute didn’t do it well consistently? On the other hand, there was another person who started out not knowing how to do it, but then, over time, built up a proficiency to pack it well every time. And that’s what I’m thinking about…I want a student to show that over time, they have built consistency in their [mathematical understanding], even if they start out not understanding how to do it.”

Even if a student starts out imperfect, Professor Reese values true learning as an increase in understanding over time. He considers mistakes an opportunity to grow, not anything a student, especially in a subject as demanding as mathematics, should be penalized for. He described his positive relationship with mistakes to me as, “One of my favorite courses I took on machine learning taught us to program the computer to go down a certain path, make mistakes, until it discovered that they road it had taken led to mistakes, and then it starts to find the optimal route; the actual best way to do things. And that’s learning, in a nutshell. You don’t learn how to walk as a kid right away. You fall down, bump your head. It’s trial and error until you realize how not to do it…and in doing so, you find the right way. You don’t learn tic-tac-toe by winning. You learn by choosing all the routes not to follow.” Retesting on mathematical standards allows students to learn from their previous mistakes and improve, not be hindered, because of them.

Developing the system, however, did not come overnight to him. He started out with a traditional grading system, like most of the rest of the educators in America. He found himself constantly questioning why arbitrary numbers governed a student’s measured performance in his classes. “I looked at so many syllabuses and saw teachers choose arbitrary numbers for certain categories, like, 10% for homework. And I kept asking, why? Why 10%? We like 5’s and 10’s so much. Why not…7%? And you start to go down that rabbit hole and really start to realize…Well, okay. Why is that problem worth 10 points and why is that mistake worth 1 point? And that’s where the system starts to unravel. There are inherent biases in that grading system, there was a choice made there. Why?” Frustrated with the lack of transparency in these systems, he decided to scrap it all and pursue a new method unlike he’d ever done before.

Why It’s Working

He described that he based the early foundations of the retest policy and his teaching style from extensive educational research done by the Marzano Research Group, which he informed me were key in providing him with insight that helped him understand how students can learn most effectively. He also reached out to and followed many other educators across the country, all with the like-minded ideal to create a grade that was best representative of the learning process. “I’ve liked this system the best because it does two things: one, it gives students ownership over their understanding. If you can reassess and find the places where you’re making mistakes…then you have more of a buy-in into what your education becomes. The second part is that it creates a growth mindset philosophy and develops grit.” Professor Reese described that he’d been heavily influenced by Dr. Angela Duckworth’s famous research on “grit” as one of the keys to success in any environment. Grit, as Dr. Duckworth describes, is “the tendency to sustain interest in and effort toward long-term goals.” In a mathematics course, this to Professor Reese means pushing on in the face of mistakes and setbacks.

Professor Reese excitedly recounted the great successes he’s had so far with his current system. “Students who are most successful look at a setback as something that is not detrimental,” Professor Reese reported, “they view it as an opportunity to grow…A mistake is an opportunity for a breakthrough.” He told me that his most successful students are the ones he finds coming back every week for reassessments to increase their mastery of the subject material, and that almost all his students showed increased proficiency with this system.

Despite his extensive research and efforts making his system the most efficient and representative of learning as it can possibly be, Professor Reese doesn’t claim his system to be perfect. “For one, it requires constant assessment.” he stated. “I need to continually be checking in to see where the students’ level of understanding is…That can take away time from instruction and it makes me wish my students and I had more time to make mistakes together in class.” Professor Reese says he still struggles with fitting his desired curriculum and practice time into the quarter system, but that his understanding of it and how to most efficiently teach increases with each quarter that he’s here. “Another drawback about having a quiz every week is if they don’t get it at first, it can be a real burden on the student. I try to balance that constant assessment with showing gradual improvement, but without that feedback about students’ understanding, I can’t see by how much their understanding has been increasing.”

From the other side of that, both my fellow classmates and I have found that constant assessment has reduced our test anxiety as a whole. When we’re exposed weekly to the stresses of test-taking, we learn study tips that help us manage this and adjust our test-taking skills accordingly. This, in turn, has reduced our nervousness for each weekly quiz, which causes us to make less mistakes in the first place due to anxiety. Math anxiety is a common issue for many students across America — could the solution to this actually be testing them more, not less? Recent psychological research suggests that the answer is yes. According to Scientific American, “Research in cognitive science and psychology shows that testing, done right, can be an effective way to learn. Taking tests can produce better recall of facts and a deeper understanding than an education devoid of exams.”

As our interview came to a close, Professor Reese elected to leave me with some closing thoughts. His first, addressing students, was, “I know it sounds cliche, but…keep trying. Keep putting in the work, even when the work’s not going well. A lack of understanding now may not mean so in the future. Failure is hard, but it’s not permanent. Don’t see a wall as blocking your path, but some obstacle you can and will overcome.” He wanted to translate this positive and introspective note to his fellow educators as well, especially when it comes to evaluating why they teach and grade the ways they do. “My advice to them would be to take a moment and actually think about why their system is what it is. When they set up a course, always revisit the ‘why.’ Even if their system is very traditional, I want them to think, ‘Well, why do I have homework as 10%? What do these arbitrary numbers really mean?’ When they start pulling on all those threads, either the whole system falls apart or they can put it back together in a way that truly represents their students’ progress. I’m not saying I’m the most innovative or perfect educator in the world…but at least I’m always questioning the ‘why.’ And I’m trying to get a little better, every week, because that’s all you can really ask for. Progress, even if it’s slow.”

And finally, Professor Reese told me he understands that not everyone is a mathematician, and success in his classes can mean very different things to different students, and he wants to be supportive of all of those definitions. “Success doesn’t necessarily mean an A to me. If you work your ass off, and you get a C and you’re proud of that, then I’m over the moon. I just want to support my students in whatever they perceive their own success to be. I’ve received emails from students who go from B’s to A’s, C’s to B’s, and failing to passing — and all make me equally happy. As long as I know they’ve really learned and reached their form of success, I’m happy.”